【神奈川県公立高校入試】数学で「65点」を突破するために

こんにちは、個別進学塾トークス平塚校の宮崎です!
神奈川県の公立高校入試(学力検査)の数学は例年、受験者平均点が50点台半ばで推移しています。
これは中堅以上の難易度の高校を目指す場合、仮に数学が苦手でも満点を取る必要はなく、
戦略的に「65点」を獲得できれば、平均点を上回ることでアドバンテージになる
ことを意味します。
中堅レベルの高校を具体的に述べると、湘南エリアでは茅ヶ崎高校、大磯高校、鶴嶺高校、湘南台高校、藤沢西高校などです。
先に申し上げておくと、神奈川県公立高校入試において数学で60点を取るために必要な能力とは、難問を解く力ではありません。
必要なことは、
・解けるはずの基本的な問題を、
・制限時間内に、
・ミスなく確実に得点する
ことです。
本日は公立高校の入試本番で65点を取るために必要な内容を深堀りしてみたいと思います。
※正確には年度によって出題される内容は異なります。あくまでも参考程度に読んでください。

個別進学塾トークス代表の宮崎です!
大手塾に勤務後、独立し茅ヶ崎市に自分の塾を開校。常に満席になることが増えたため、2教室目として平塚市に個別進学塾トークスを立ち上げました。
10年以上の指導歴があり、数百名の合格者を出している、神奈川県の高校受験・大学受験の専門家です。
神奈川県高校入試の数学の「問題構成と難易度」を分析する

神奈川県の入試問題は、毎年出題形式や構成が非常に安定しています。
50分という限られた時間で得点を最大化するためには、過去問を単に解くだけでなく、問題の構成とそれぞれの難易度を正確に把握し、事前に「解くべき問題」と「解かない問題」を分類しておくことが不可欠です。
入試問題は、難易度別に大きく以下の3つのグループに分類できます。
入試数学グループA <基本問題>
問1・問2の問題群で、配点目安は約35〜40点です。
受験者の多くが正解する、最も基本的な領域です。
65点確保のためにはここでの失点は防ぎたいので、最優先で取り組みたいですね。
問1(計算問題):
正負の数、文字式、平方根などが出題されます。数値設定は単純で、教科書の例題レベルです。
1ミス=内申1ポイント減と同じ価値ですから、計算ミスは避けたいですね
問2(小問集合):
連立方程式、二次方程式の解、関数の変域、確率の基本、平面図形・空間図形の基本などが出題されます。
複数の単元がランダムに出題されるため、それぞれの基本解法を即座に引き出す知識の定着度が問われます。
入試数学グループB <標準問題>
問3(ア)(イ)と問4〜6の(ア)が該当する問題群で、配点目安は約20〜25点です。
問4以降は応用問題の一部ですが、問われている内容は基礎知識の活用であり、そこまで難易度は高くありません。
合格者平均点(50〜60点)を目指す場合、ここまでを確実に得点する必要があります。
問3(ア)(イ)(図形・対話文など):
近年では、会話形式の問題や、箱ひげ図(データの活用)、円周角の定理を用いた問題が出題される傾向にあります。
問題文が長い(文章量が多い)ですが、論理構成自体は標準的です。
問4〜6の(ア)(関数のグラフ・確率・空間図形):
各大問の最初の設問です。
大問に含まれているため難しく見えますが、実際には「関数の式を求める」「基本設定に基づいた確率を数える」といった導入問題です。
問2(小問集合)と同等か、それ以上に解きやすい場合が多く、得点源となります。
入試数学グループC <応用問題>
問4〜6の(イ)(ウ)などの問題群で、正答率が低く、解法に複数の手順を要する問題群です。
65点を目標とする場合、これらの問題への対策は優先順位を下げてよいでしょう。
もちろん数学が得意だったり、正答率が高い場合には練習を重ねて得点源にしても構いませんよ。
問4〜6の(イ)(ウ)
図や表から、
「面積を2等分する複雑な直線の式を求める」
「立体図形を切断した際の体積比や線分の長さを求める」
といった内容になっています。
これらの問題は(65点を目指す人にとっては)手順が複雑かつ計算量が多く、処理に時間がかかるため注意が必要です。
入試で点数が伸び悩む原因の多くは、
・「グループA(基礎)」での決定力不足
・「グループC(難問)」への過度な時間配分
です。
神奈川県の数学入試では、難問を解いた場合の得点も、基礎問題を解いた場合の得点も、配点に大きな差はありません。
湘南エリア中堅の高校(茅ヶ崎高校、大磯高校、鶴嶺高校、湘南台高校、藤沢西高校)を目指す戦略においては、グループCの問題に取り組む時間を、グループA・Bの見直しや検算に充てるほうが、最終的な得点は高くなると僕は考えています。
いずれにせよ、問題構成を理解し、自身の目標点数に合わせて解く問題の優先順位を確立しておくことが重要だといえるでしょう。
神奈川県高校入試の数学で65点を取るための戦略

実際の入試では50分という限られた時間での戦いになるわけですから、どの問題で得点するかをある程度決めておけると良いですね。
以下の問題は、正答率が高く(=多くの受験生が正解する)、難易度も標準的です。
これらをすべて正解できると、6割に届きます。
ここでは例として、2025年度入試で考えてみましょう。
問1:計算(15点/5問正解)
正負の数、文字式の計算、平方根など、中学校の小テストレベルの問題です。
全問正解を目指しましょう。

問2:小問集合(20点/5問正解)
連立方程式、二次方程式の解、求角、資料の活用、変化の割合、基本的な確率、簡単な文章題など、各単元の基本が凝縮されています。
問題のバリエーションが多いですが、難易度は比較的低めです。
2025年度においては(エ)一次方程式の文章題、(カ)回転体の体積の正答率がやや低めでしたが、決して高いレベルではありません。
キチンと得点を狙い、ミスを1問以下に留めましょう。

問3:小問集合+(10点/3問正解)
小問集合ではありますが、文章量や図表が多いです。
難易度は標準〜難しめのレベルで、キチンと解こうとすると時間と体力を削られます。
2025年度では(ア)(i)a、b、(イ)の3問を正解させると10点分となります。
内容はそれぞれ平面図形の面積と証明、箱ひげ図でした。

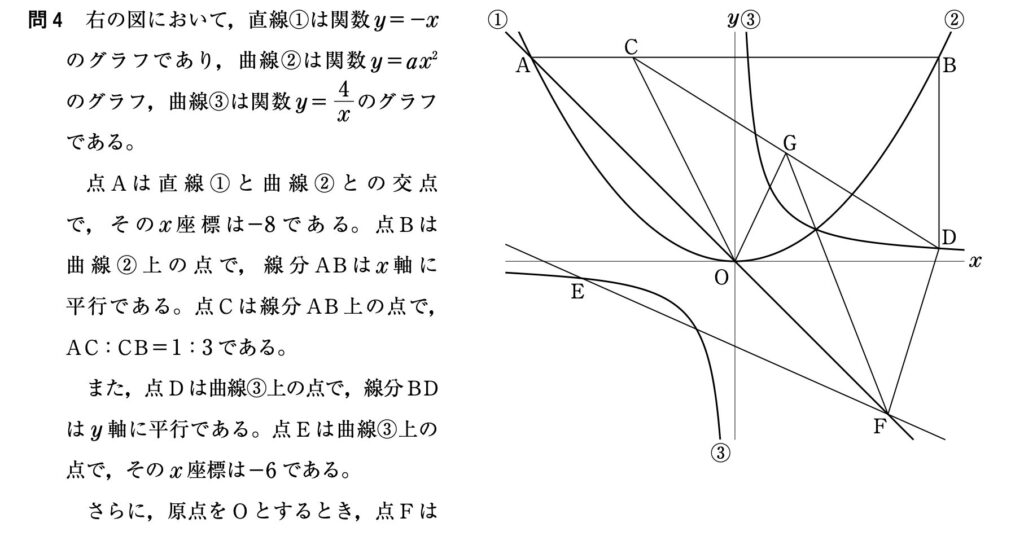
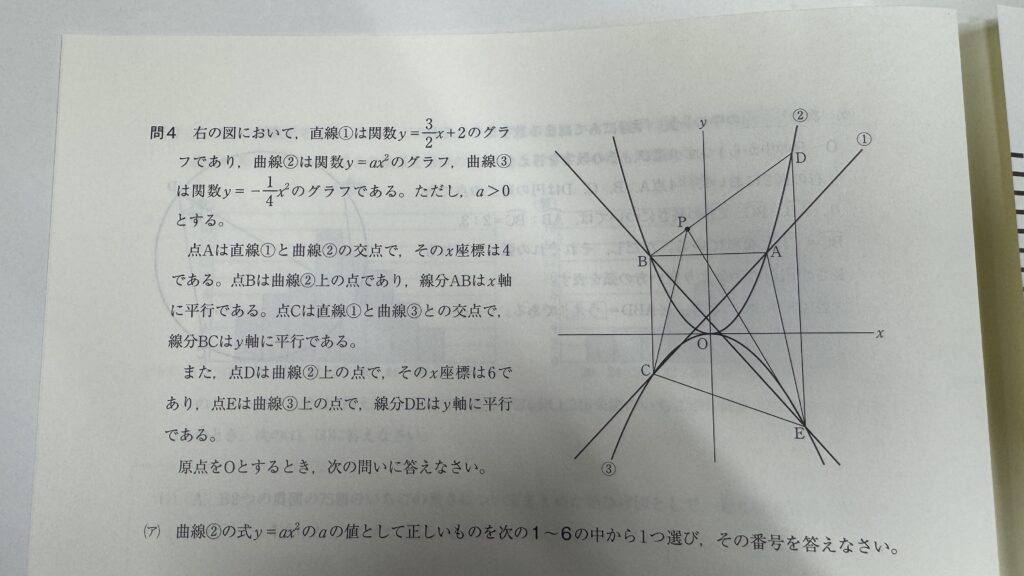
問4:関数(9点/2問正解)
(ア)(イ)の2問を狙いましょう。
(イ)の難易度は年度によってバラツキがありますが、練習段階では解けるようにしておきたい1問です。
(ウ)の正答率は例年10%以下なので、いったん無視しても構いません。
問5:確率(5点/1問正解)
問題文が長く、一見すると難しそうですが、実は問題自体の中身はそこまで高くありません。
(ア)のみ正答で5点取得できます。
練度次第では(イ)も正解できるぐらいのレベル感なので、練習段階ではトレーニングしておけると吉でしょう。

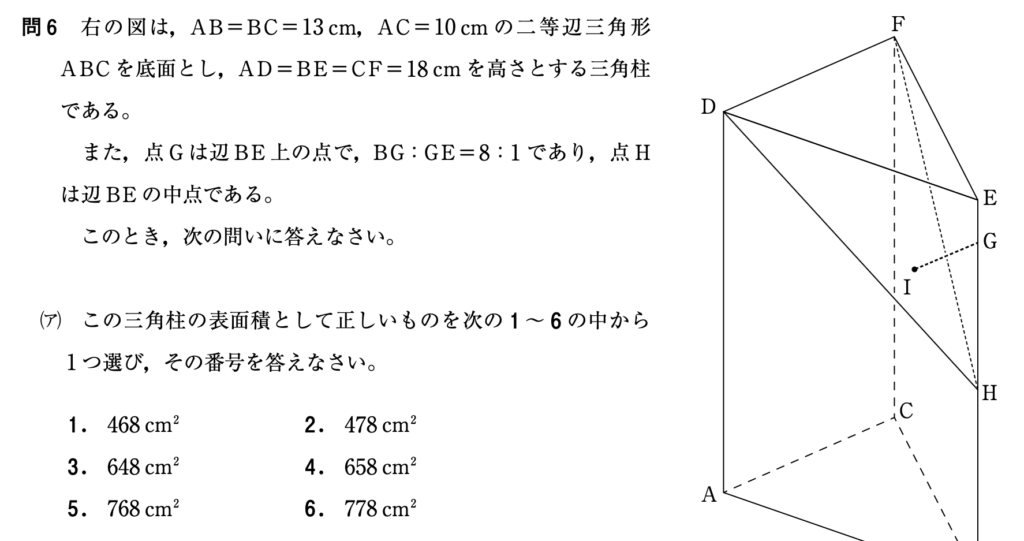
問6:空間図形(4点/1問正解)
立体的な図形を切ったり、立体物に紐を巻いたり、展開図を組み立てたりする問題です。
図形の知識を組み合わせれば解けることが多いため、練習さえしておけば(ア)は比較的解きやすいですね。
(イ)はひとまずスルーしましょう。
問1〜6で、それぞれ15点、20点、10点、9点、4点、5点を取ると、合計で63点となります。
この中から図形問題をすべて捨てたとしても55点取れるので、数学が苦手だったり図形問題に抵抗があったとしても、ある程度の点数は確保できます。
神奈川県の公立高校入試における数学は、他の科目と比べて練習した分だけ点数に反映されやすい科目です。
教科書や塾のテキストでの復習はもちろん、模試や過去問を上手に使うことで点数を上げやすくなるので、受験期には優先的に勉強時間を割きたいところですね。
あ、ちなみに僕たちの個別進学塾トークスでは模試や過去問だけでなく、予想問題も使ったりしてます。

けっこう当たるんですよね、この予想問題。
中堅高校を目指している多くの受験生が「応用問題が解けない」と悩みますが、実際には問1の計算ミスや問2のうっかりミスで10点、15点と失っています。
本来正解させるべき問題での計算ミス・問題の読み落としを誘発する…これは最悪のパターンです。
何度も言いますが、入試は「解ける問題」を確実に取り切った人が勝ちます。
難問ではなく、解ける問題をしっかり拾えるように鍛えましょう。
神奈川県高校入試の数学「65点戦略」の勉強法

上記で解説したように、公立高校入試の数学で65点を取るための難易度は決してハイレベルではありません。
ですが、なんとなく勉強しているだけでは届かない点数でもあります。
ここからは、65点を狙うにあたって意識しておきたい勉強方法についてお伝えします。
ある程度の問題まではスラスラ解けるように、効果的なトレーニングを積み重ねましょう。
計算力の徹底強化
単純な計算問題を間違えてしまう理由は、ルール通りに解いていないかルールを知らないかの2択です。
計算ルール通りに解かないとは、たとえば途中式を書かなかったり、字を汚く書いてしまうことも含みます。
僕たちが口うるさく「途中式を書け」というのは、
・先生が見やすいようにしろ
という意味ではなく、
・脳のメモリを解放してエラーを減らすため
なんですよね。
途中式を書かずに頭の中で計算すると、情報処理の負荷が上がります。
xを左辺に移項して、-3yと+4を右辺に移項して、両辺に-4/5をかけて、カッコを外して…
という作業を一度に、しかも何にも書かずに処理したら、そりゃエラーも出ますよね。
一つひとつは簡単な作業でも、頭の中で同時に、となると正答率は一気に下がります。
反対に、途中式を書いたり文字を丁寧に書くと、情報処理の負荷が下がって頭の中のメモリが空くため、間違いは大きく減ります。
ずっと勉強に携わっている僕ですら、計算するときには未だに途中式を書きます。
その方が楽なんですよね、余計なことを考えなくていいので。
途中式を書いたり文字を丁寧に書かない人の心理は、面倒くさい・何も考えていないか自信過剰かのいずれかです。
ルール通りに取り組めば間違えないものを、自分自身の感情からミスを誘発してしまう。
入試数学で60点を確実に取りたいなら、感情に惑わされず手順通りに計算しましょう。
一方、そもそも計算ルールを知らないのであれば、当該学年に戻ってインプットし直すことをおすすめします。
以下に内容と学年を列挙しておきます。
| 小学校 | 中学1年生 | 中学2年生 | 中学3年生 |
|---|---|---|---|
| 小数 約数・倍数 分数 | 正負の数 文字式 一次方程式 | 単項式と多項式 等式変形 連立方程式 | 展開・因数分解 平方根 二次方程式 |
入試数学で60点を目指す受験生の中には、計算のルールについて自信を持って説明できない人もいます。
はっきり言っておきますが、計算が不安定だと60点はかなり厳しいです。
他の勉強を進める前に、あるいは他の勉強と並行しながら、絶対に計算問題を100%正解できるようにしておきましょう。
いくら文章題から立式できたとしても、途中の計算を間違えていたら0点ですからね。
そして、計算問題において最終的に目指す状態とは
・(計算問題は)考えずに解答できる
という状態です。
いちいち考えない。いちいち感情を入れない。
数字を見て、機械的に算出して、100%正答する。
単純な計算問題をクリアするために、この状態を目指しましょう。
基礎と実践の反復
基礎は大事とよく言われます。これは間違いありません。
ただ、同時に実践力も重要であることを忘れてはいけません。
いくら基礎力を高めても実践力がなければ、本番で点数が取れないからです。
「基礎を徹底すれば6割は取れる」のは学校の定期テストまでであり、高校入試でも大学入試でも、6割を安定して取るためには標準レベルの問題と対峙する必要があります。
ここで言う実践力をつけるためには、
・学校の教科書の章末問題
・学校ワークのC問題(入試問題に挑戦!のページなど)
・塾のテキストの標準問題
といった問題を解くことが有効です。
これらの問題を見た瞬間に解法が思いつくかどうかが勝負の分かれ目になります。
考える力を鍛えるというよりは、解法パターンの引き出しを増やして即座に取り出せるようにするという練習ですね。
具体的な練習方法を以下に述べます。
①「縦(タテ)解き」でパターンを刷り込む
単元ごとに集中して解く練習です。
「今日は関数だけ」「今日は確率だけ」と決めて、北海道から沖縄まで、あるいは近隣の県の同じ単元の問題だけを10〜20問連続で解きます。
連続で同じジャンルの問題を解いていると
・またこのパターンか、さっきと同じだ
・この問題は変域が変わるだけだな
という出題のクセが見えてきます。
すると脳がその単元のモードになるため、記憶の定着率が格段に上がります。
この「縦解き」トレーニングは知識の定着に最適です。
ある程度進んだら、次の練習も取り入れてみましょう。
②「1行目」を瞬時に出すトレーニング
入試問題が解けない原因のひとつに、「えーっと、これどうやるんだっけ?」と悩みすぎてしまうことが挙げられます。
そのため、問題文を読んですぐに解き方を思い出せるよう、手を動かさずに「解き方の方針」だけを答える練習を行うことも大事ですね。
問題文を読んで10秒以内に、
・これは三角形の相似を使って比を出すパターンだ
・これとこれで連立方程式を立てる問題だ
と言語化し、そしてすぐに解答を見て方針が合っているか確認するトレーニングに取り組みましょう。
ポイントとしては、実際に計算はせずに方針が合っているかをチェックすることです。
方針が出なかった問題は、解説を読み込んで「何に注目すればその解法が思いつくのか」を確認します。
これを繰り返すことで、問題文を見た瞬間に解放が頭に浮かぶようになります。
いかがでしょうか。
これらの練習に取り組むときは、先ほど述べた学校のワーク類だけだと練習量が不足するため、
・全国高校入試問題正解
・都道府県別の過去問
・塾専用教材(極める神奈川/県トレなど)
といった、受験に特化した教材があるとトレーニングしやすいでしょう。


特に練習におすすめなのは塾専用教材で、単元ごとに問題がまとまっていながらもボリュームもあります。
正直、これ1冊と過去問だけで模試の偏差値が5〜10アップすることも珍しくありません。
実際に僕たちトークスの教室でも受験対策の教材として重宝しており、中学3年生の夏以降は積極的に使っています。
極める神奈川や県トレなどの塾専用教材は、入試問題にそっくりな問題ばかり載っているため、「縦解き」「1行目」トレーニングの両方で活用できます。
(もし受験や勉強について不安がある場合は、どうぞ平塚市・茅ヶ崎市の進学個別塾トークスまでご連絡ください。)
上位校(特色検査実施校の平塚江南・茅ヶ崎北陵・鎌倉高校あたり)を第一志望にする場合は塾専用教材だけではなく、全国高校入試問題正解も併用するといいですね。
過去問とは出題パターンが違ったり、過去5年間で出てきていないケースの問題にも対応する必要がありますから。特色検査で使う思考力の練習にもなります。
神奈川県の数学入試で65点を狙うための定着目標としては、
関数
交点の座標を求める、三角形の面積を2等分する直線の式を求める
平面図形
円周角の定理を使った角度計算、基本的な証明(穴埋め含む)
空間図形
展開図から最短距離を求める、基本的な体積・表面積
確率
サイコロ2個、硬貨投げなどの樹形図を書けば解けるもの
データの活用
中央値、最頻値、箱ひげ図の読み取り
これらの問題に対して、時間をかければ解ける状態ではなく作業として処理できる状態を目指せるといいですね。
各分野、得意不得意あると思うので取り組みやすいところから始めてみましょう。
入試は「解ける問題」を拾った人が勝つ
中堅〜上位校を目指す受験生の多くが「応用問題が解けない」と悩んでいるが、実際には問1や問2のミスで10点以上失っているケースが多々ある、ということを伝えてまいりました。
散々述べていますが、入試で勝つのは難問が解ける人ではなく、誰でも解ける問題を絶対に落とさない人です。
基本問題〜実践問題を徹底的に反復し、戦略的に65点を勝ち取りましょう!
本日もご覧いただき、ありがとうございました!
こちらに勉強・受験に役立つ記事などをまとめました◎
●神奈川県の公立高校紹介

●神奈川県入試のしくみ

●文字数42,000文字以上の
『成績アップの教科書』配布中!

●個別進学塾トークスの受講生実績

●個別相談・体験授業はこちらから!

成績アップと志望校合格を目指すなら、高校受験・大学受験に強い、平塚市・茅ヶ崎市の進学型個別指導塾トークスへぜひ一度ご相談ください。
これからも個別進学塾トークス平塚校では、平塚市、茅ヶ崎市、藤沢市、大磯町に住んでいる小学生・中学生・高校生の勉強や受験について、役に立つことをお伝えしてまいりますね!


